Facts about Canada’s
Energy Industry

Hydraulic fracturing, or fracking, is a proven and highly-regulated technique that has been used by oil and gas companies for over 60 years.

Fracking follows the basic principle of cracking rock and propping it open to allow oil and gas to flow to the surface. Though the principle is simple, continuous innovation has led to the development of highly-advanced technologies that have enabled access to vast new oil and gas resources and spurred new production growth – especially over the past 15 years.

What is Hydraulic Fracturing or Fracking?

Contrary to popular belief, fracking is not a drilling process. Fracking takes place after the well has been drilled, cased and cemented. Fracking is a process that uses fluid to stimulate the flow of oil and natural gas to the surface of the well.

Fracking is a carefully-designed process that considers many conditions prior to initiating the treatment, including the following:

• Type of rock in the formation
• Depth of the well
• Downhole temperature

These conditions and additional properties are modeled with a computer to illustrate the expected dimensions of the fractures that will result from the proposed treatment. With these details, a plan is developed to optimize the performance and mitigate potential risks during fracking operations.

In the field, the fracking process will take 3 to 4 days per well and involves the following basic steps:

1. Water, proppant (frac sand) and chemicals are transported and stored at the wellsite. Frac equipment arrives and is set up.
   Note: Graphic being upgraded by Streamflow
   
   

   Photo credit : Trican

2. Frac fluid, also known as hydraulic fracturing fluid or slick water, is mixed onsite, and frac pumpers pump the fluid into the well at a pressure high enough to create small (millimeter-scale width) cracks in the targeted rock formation deep below the surface.

   Once the interval, or stage, is adequately fractured, pumps are shut down, the pressure is reduced and the cracks begin to close. The frac sand “props” open the fractures to allow the hydrocarbon molecules to flow into the cracks and then to the well.

   Fracking typically starts at the toe, or end of the horizontal leg, and works back to the vertical part of the well. The process is referred to as multi-stage hydraulic fracturing. Commonly it takes an average of 10 to 15 stages to ensure adequate coverage of the reservoir to maximize the recovery of the oil or gas it contains. The number of stages depends on the lateral length of the well.

3. Completing the planned stages usually takes about 3 to 4 days. Then fracking equipment is removed from the wellsite and flow-testing and/or production equipment is installed. Now oil or natural gas will be able to flow from the well.
4. Initially, the oil or gas is allowed to flow from the well along with the majority of frac fluid, referred to as flowback fluid. The flowback fluid is separated from the natural gas or oil and stored at the wellsite. The well can flow (or produce) for years, but the flowback of fluid only occurs over days or months. 

   The carefully recovered flowback fluid is either reused for another well or disposed in government-approved facilities. Operators must track flowback fluid volumes and report them to regulators.

Frac Fluid

The choice of frac fluid is dependent on reservoir properties, cost and availability. 

The frac fluid used during the fracking process consists of:

• A base fluid: most commonly water, but can also be liquid carbon dioxide (CO₂) or nitrogen (N₂)
• Proppant or frac sand: commonly pure silica sand, but can also be resin-coated sand or ceramic beads 
• Additives: common additives that change the performance of the fluid throughout the fracking process and protect the reservoir and equipment

Frac Fluid = Base Fluid + Proppant + Additives

Source: Trican

Frac Fluid Disclosure

Canada’s oil and gas industry understands that the public has questions about the additives used during fracking and therefore is committed to public disclosure of the frac fluids they use. The vast majority of additives used in frac fluids are also used in common industrial and household processes such as shampoo, lipstick, antiperspirants and ice cream. 

Service companies that conduct fracking in the field are committed to providing exploration and production (E&P) companies, their clients, a list of additives used in their frac fluids.

In turn, E&P companies are committed to public disclosure of additives used to fracture the wells they own. FracFocus hosts a public registry where companies upload data about their hydraulic fracturing operations in Canada.

Ensuring Fracking is Safe and Responsible

Continuous, real-time monitoring of fracking operations is key to ensuring worker and environmental safety. Fracking operations involve a well-trained workforce that blends the fluid and monitors pumping pressures, rates and volumes to ensure fracking activities follow the designed, site-specific plan. Pumping equipment can be stopped at any point if the operation varies from the plan or if a stoppage is required for any other reason.

Micro-seismic monitoring is the real-time monitoring of the induced seismicity that occurs during fracking. Micro-seismic monitoring creates an image of each frac stage so that the operator can be sure that the fracking process is occurring as intended within the targeted rock formation.

The monitoring delivers information about the changing stress of a reservoir. From this data, operators can demonstrate how far cracks extend. The cracks grow more in the horizontal direction than they do in the vertical direction. For example, fracs in the Horn River Basin of northeast British Columbia can extend hundreds of metres laterally and tens of metres vertically.

Source: Trican

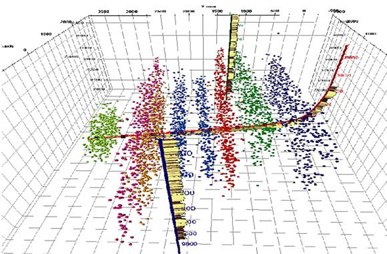
Source: Schlumberger

Source: Schlumberger

Fracking, like all oil and gas activities in Canada, is strictly regulated. Every phase of oil and gas development must apply for regulatory approval before work can begin.

In addition to regulations, the Canadian industry and government personnel have worked together to develop Industry Recommended Practices (IRPs) for fracking. IRPs are developed through collaborative efforts and they identify best practices for preventative measures to mitigate risks during fracking operations.

Finally, not all of industry’s work is done in the field. Many hydraulic fracturing companies have state-of-the art research and development centres focused on continuously improving fracking techniques.  The work in these labs is leading to advances at the wellsite in the following areas:

• Environmentally-friendly fluids, green chemicals and new technologies that will allow fracturing with less freshwater
• Tracer systems used to evaluate fracture distribution and productivity
• Downhole monitoring techniques to enhance the effectiveness of each frac stage
• Innovations in the reuse and recycling of frac fluids

Source: Trican